《系统级汽车架构安全分析方法（3）》描述如何实现模型综合（从汽车网络架构中合成CTMC连续时间马尔科夫链），重新迭代了概率模型检查的基本内容，并重点检查了不同组件的性能影响。本文将介绍汽车网络分析所需的属性规范子集。在确定模型综合和属性后，对模型进行属性分析。

01属性规格

为了评估上一篇中合成的模型，需要指定一个属性。然后通过模型检查算法对模型进行属性检查。通常情况下，可以定义大量的多样化属性。一般采用一种语言，如计算树逻辑(CTL)来形式化描述属性。可以验证的属性非常灵活，除此以外，还包括可到达性和系统在某一组状态下停留的时间。

对于SAAN（汽车信息安全分析：一种在系统级对汽车架构进行安全分析的方法和框架）来说，关注的是系统、子系统、组件或这些集合的可被利用的时间。为了确定这一点，我们需要将分析时间  和关注的状态  定义为属性  。

          (3,24)

当直接定义时间  时，定义有关状态为向量  。为此，我们将待分析的组件表示为  。由于可被利用性对应于给定系统保持在单一状态或一组状态的时间，我们将这些状态集合，表示为一个向量  。向量  的长度与系统的状态数量相同。  。对于每一个要分析的组件的子状态  (见下图1.3)，如果该子状态是可被利用的，则向量中的相应值设为1，否则为0。

（a）瞬时变换

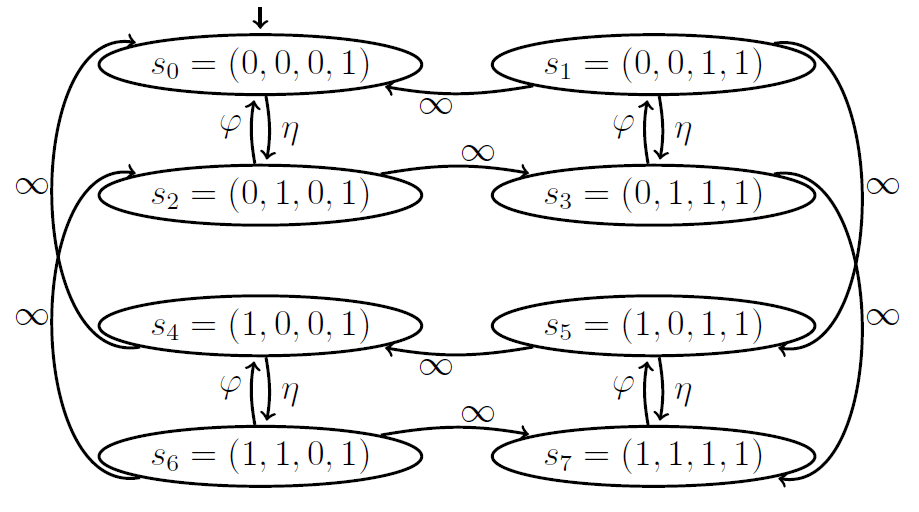
（b）非瞬时变换

图1.3 通过图1.2中的体系结构生成了具有瞬时变换的通用Markov模型（a）和不具有瞬时变换的优化Markov模型。状态表示为：  ，其中  表示输出接口的状态，  表示输入接口的状态，  表示ECU的状态，  表示总线的状态。可被利用率为  ，修补率为  。

               (3,25)

               (3.26)

当对图3.6(b)中，我们的例子中ECU的状态进行可被利用性分析时  ，可得   和  。

接下来，将介绍模型检查算法，验证模型的属性，并将合成的模型和属性规范作为输入。

02模型检察

在《系统级汽车架构安全分析方法（3）》中确定了要分析的模型，并在上文中给模型指定属性后，现在，将对指定属性  的模型进行分析。

此处重点要介绍的是CTMC的概率模型检查。在下文中，CTMC模型检查所需的元素，经过调整和简化呈现在公式(3.27)至(3.34)中。在此过程中，一些元素会突出显示，这些元素至关重要。

为了模型检查算法，需要输入表示模型的矩阵  以及要检查的属性  。属性  包含向量  ，表示待分析的状态集和分析时间框架  。矩阵  表示状态的变换，状态  变换到状态  时，分配在矩阵中的坐标为   ，变换率用  来表示。从  到  的变化表示为  。状态之间不存在变换时，转换率为零，并相应设于  中。此外，还要求矩阵的行相加为零。因此，  处的值设为行中所有项的负和。

            (3.27)

下面，我们将简要探讨图1.3(a)中的通用方法和SAAN方法的矩阵生成，分别表示为  和  。可被利用率和修补率表示为  。对于通用方法（如图1.3(a)），需要近似地计算无限变换率。在下文中，我们使用的值是10。图1.3(a)和(b)中，最小的例子所得到的矩阵分别用公式(3.28)和(3.29)来表示。

       (3.28)

                     (3.29)

要在给定的时间  内，检查CTMC的模型矩阵，首先需要将矩阵  正规化。为了实现这个目的，将矩阵  除以  ，也就是一个状态的所有输出变换的最大值。这个值可以作为  中所有值的绝对最大值。

             (3.30)

由于该应用包含的始终是阳率，所以  不需要考虑。

得到矩阵   ，其中  为单位矩阵，表示分析后的CTMC中嵌入的DTMC（离散时间马尔科夫链）。由于  考虑的是在单个时间步的所有变换率，因此  考虑的是  个时间步内状态间的所有转换率。

在 CTMCs 中假设指数分布，可以用来模拟变换。为了模拟这种指数行为，在每个步骤中都采用了泊松分布（  ）。将分布的参数设置为  和  ，由此得出模拟带有  的变换率，在  内触发  次，如需对指数行为建模，就需要累计泊松概率。

这样，我们可以计算出时间  内的变换矩阵。

         (3.31)

但是，通过这种矩阵还不能直接知道时间  后单个状态的概率，因此，通过将向量  的相应值设为1，创建向量  来选择有关的状态。可以得到：

        (3.32)

且

       (3.33)

最后将预期值定义为：

     (3.34)

接下来简要讨论这种计算的性能影响：

性能影响。公式(3.34)中的计算被定义为无限和，但实际上，这种计算必须是有界的。在其他文献中，有提到一种算法是用来确定达到设定精度所需的最小和最大迭代次数。对于大的  ，迭代次数被定义为与  成线性比例，如果存在瞬时变换，根据定义，则形成系统中最大的速率。这就导致公式(3.34)中的迭代次数增多，计算时间更长。这种依赖性清楚地表明了瞬时转换的大近似对模型检查算法计算时间的影响。因此，  应尽可能地保持较小。

此外，当系统中最小的和最大的速率相差太多时，过大的瞬时变换近似值会导致模型形成一个刚性模型，在此设置中，大约是7个数量级或以上。然而，太小的近似值会导致不准确的结果，因为太小的近似值不能准确的表示实际情况。在任何情况下，瞬时变化都会产生更大的  ，减缓模型检查。本文提出的SAAN消除了瞬时变换，从而提高了模型检查的效率。

模型大小。如公式(3.28)和公式(3.29)所示，通用方法建立的模型明显大于特定领域方法。分析较大的模型会增加分析时间，因为公式(3.34)中的矩阵乘法需要的时间明显延长。去掉瞬时变换可以减小模型的大小，从而使模型分析所需的计算量最小化。这点将下篇文章中分析。