《系统级汽车架构安全分析方法（2）》介绍了用于汽车网络概率模型检查的方法——SAAN，并利用定义的汽车架构知识，减少了建立的马尔可夫模型大小。从该方法的结果来看，似乎没有什么难度，但建模中的状态空间满溢等方面却使方案的实施困难重重。本文将描述如何实现模型综合（从汽车网络架构中合成CTMC连续时间马尔科夫链），重新迭代了概率模型检查的基本内容，并重点检查了不同组件的性能影响。

01模型合成

为了更好地理解模型合成中会遇到的问题，在此举一例说明。

这个例子描述了一个最小的系统，该系统包括一个通过接口连接到一个总线上的单一ECU（如下图1.1）。请注意，我们将接口  分为输入  接口和输出  接口，以证明SAAN的建模灵活性。

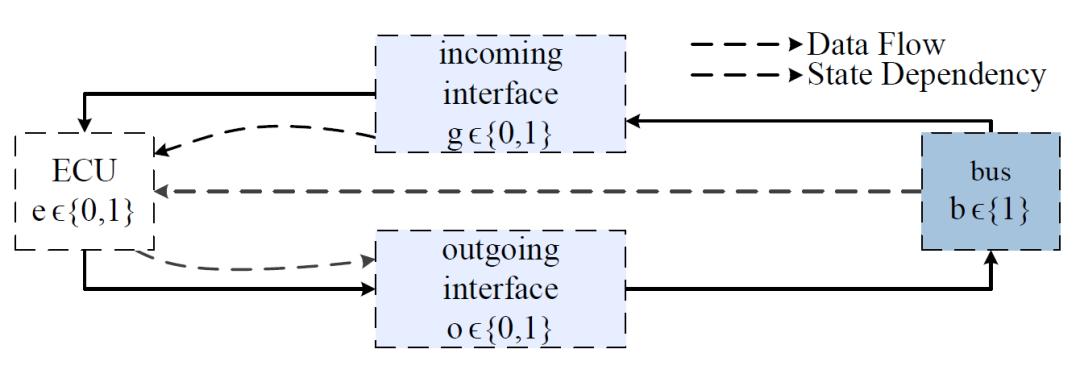
图1.1 包含ECU和总线的车辆网络以及ECU的输入和输出接口的最小工作示例。注：每条路径的数据流都是单向的，安全状态的相关性以虚线给出。

本例显示了通过输出接口从ECU到总线的数据流，以及通过输入接口从总线到ECU的数据流。此外，还描述了安全依赖性和状态，以及漏洞的数量。

在上图1.1中的例子中，除了总线外，每个组件都有两种不同的状态，即安全(0)或可被利用(1)。每个设备可能有多个漏洞，但为了简洁起见，本例中省略了这种情况。总线代表了一个组件，这个组件始终处于可被利用的状态(1)。这表示与互联网的蜂窝连接本身不具备任何信息安全性。在我们的例子中，永久可利用的总线构成了进入ECU的攻击路径。

数据流中前面组件的利用次数直接决定了输出接口  、ECU  和总线  的被利用次数。对于输入接口  ，状态只随着被利用率和修补率  和  而变化（详见前篇文章：系统级汽车架构安全分析方法（2））。被利用率和修补率定义了在给定时间内发现漏洞的频率和修补漏洞的频率。输入接口的状态对其邻居节点没有直接依赖性。

上述的架构，描述的是单个组件及其依赖关系。然而，模型检查所需的CTMC是所有组件和互连的状态的组合，全时描述完整的系统。当从这些描述中合成CTMC时，由于单个组件的行为严重依赖于其连接的组件，问题也就随之出现。

一般方法。下文描述了在排除第3.4.1节中定义的汽车系统行为的情况下，CTMC的综合方法。图1.2比较了这两种方法。当用这种一般方法生成系统的CTMC时，通过所有可能状态的笛卡尔积组合，模型出现8种（  =8）状态（见图1.3(a)）。总线对状态数没有影响，因为总线只有一个可能的状态。状态之间的变换是基于单个组件所定义的被利用率（  ）和修补率（  ）来确定的。我们将其作为基线，与我们提出的领域知识方法进行比较。

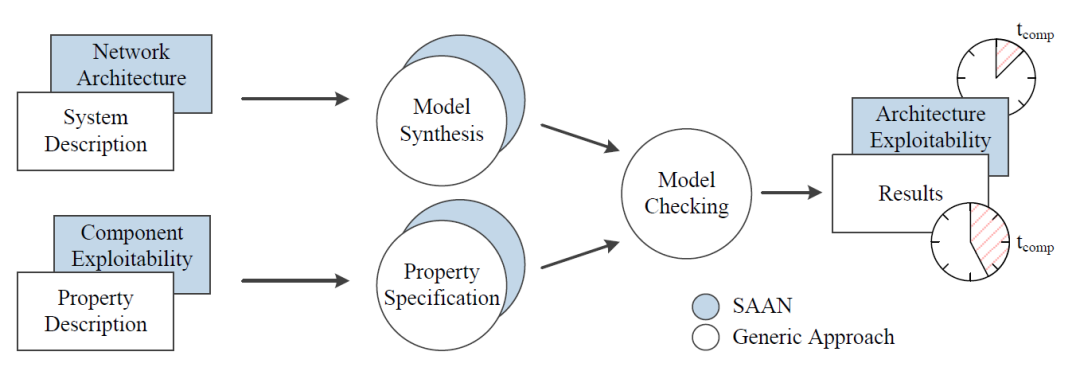
图1.2 SAAN与一般概率模型检查器的关系。SAAN实现了一种新颖的自动模型合成和属性规范。这些方法使用有关输入参数的领域知识，因此更加高效，允许模型合成和检查的速度比现有方法快三个数量级  。

（a）瞬时变换

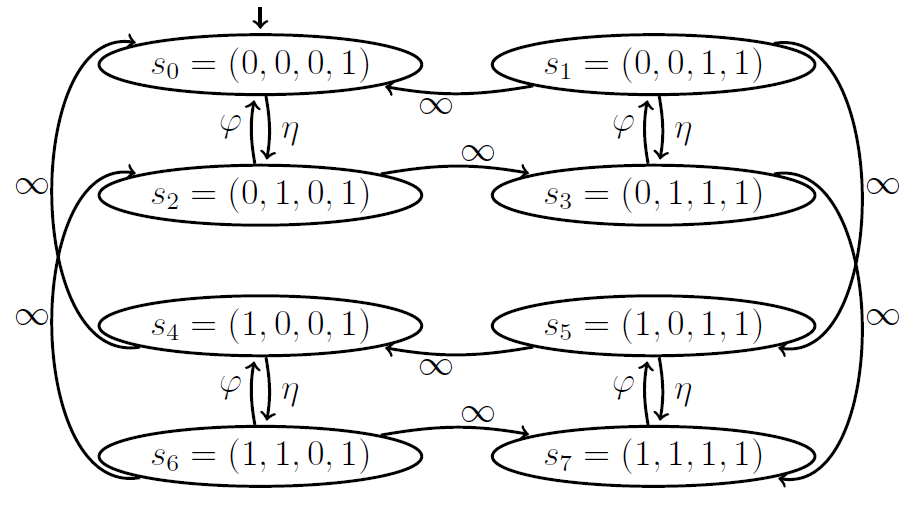
（b）非瞬时变换

图1.3 通过图1.2中的体系结构生成了具有瞬时变换的通用Markov模型（a）和不具有瞬时过渡的优化Markov模型。状态表示为：  ，其中  表示输出接口的状态，  表示输入接口的状态，  表示ECU的状态，  表示总线的状态。被利用率为  ，修补率为  。

瞬时变换。请注意图1.3(a)中的变换。一些组件的状态被定义为紧随着其他组件的状态（比较图1.2中的状态依赖性）变换，但在模型中作为单独的中间状态存在。为了连接这些中间状态，把这些状态之间的变换速度定义为无限速率（  ）。我们把这些具有无限速率的变换称为瞬时变换。这些变换只存在于笛卡尔积产生的中间状态的连接中，并不直接影响系统的行为。为了能够计算模型，需要用大值来逼近这些变换。选择的近似值对模型检查的性能有很大影响。我们将在下文中更详细地讨论这种影响。

SAAN。虽然一般的模型建立方法是基于系统中所有组件的组合，但对描述系统的最小状态集进行操作更为有效。而本文所建议提出的SAAN方法，不但能够遵循这种高效的方法，还可以利用车辆中各部件的结构、行为和关系的知识，将概率模型缩小到最小尺寸，也就是将可能出现的状态模型数量减少到最少。

首先，以规则的形式分析和定义组件与其邻居之间相关的行为。然后，定义模型的状态。基于所有组件状态的笛卡尔乘积，并利用规则集，进行模型还原，以达到最终的状态集。然后，添加状态之间的变换，从而得到最终的CTMC模型。下文将解释这些步骤。

规则。规则定义了组件的行为，如图1.1所示。公式(3.16)~(3.19)是表示系统中所有子状态的规则。本文中对组件行为的定义，是基于对行为的分析（在上篇文章中已介绍过行为的分析）来定义的，该定义表示了一个组件的新的子状态，这个新的子状态是取决于它的前子状态以及它的邻居节点状态的。为了减小模型的体积，我们计划使用瞬时变换，而不考虑通过被利用率（  ）和修补率（  ）的变换。

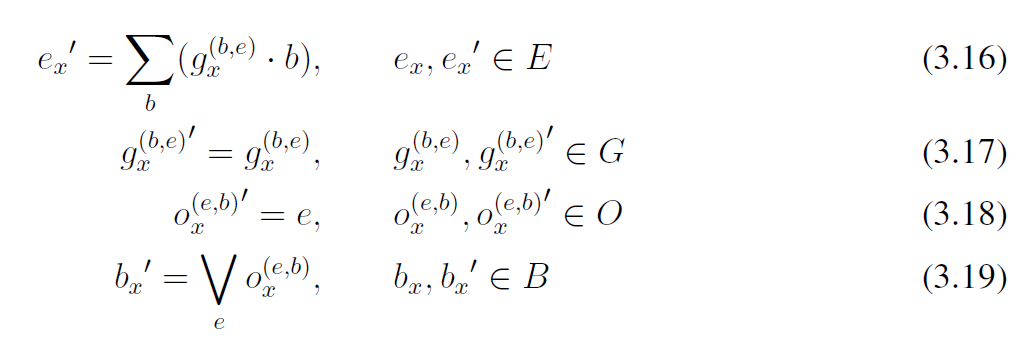
根据组件的状态，新状态  中的子状态定义为   。这个新的子状态  依赖于组件的前一个子状态(在输入接口的情况下)或连接组件的前一个子状态(在所有其他组件的情况下)，如图1.1所示。ECU   始终是一个被动元件，它的状态跟随所有连接的输入接口和连接的总线的状态（方程式（3.16））而变动。而输入接口  又不受任何连接的组件的影响(方程式(3.17))。而输出接口  的状态基于ECU的状态(方程式(3.18))，总线  的状态基于所有输出接口的状态(等式(3.19))。

虽然方程式（3.19）表示了总线的一般行为，请注意，在我们的最小例子中，总线是始终保持可被利用的，因为总线形成了攻击路径：  

从上面的规则可以看出，输入接口是唯一一个不会瞬时依赖其他接口的组件，因此，漏洞的可利用率  和修补率  可应用于输入接口。这就模拟了攻击者只能通过输入接口对ECU进行攻击的行为。如果出现多个输入接口的情况，则有可能出现具有不同数量的漏洞的多种攻击路径。

初始状态。每个组件都包含一个初始状态。对于大多数组件来说，这个状态属于安全状态（0）。然而，有些组件，如蜂窝连接，我们认为可能是可被利用状态（1）为初始状态，甚至包含不断被利用的状态，如图1.1中的总线。系统的初始状态，正是由所有的组件初始状态集合来构成的。

状态减少。为了提高模型检查方法的效率，我们应用上面定义的规则将模型种类减少到最少的状态数。在表示系统无瞬时变换行为的最小状态集时，可以通过计算减少所有瞬时变换的状态集来实现。公式（3.20）通过创建所有组件状态的笛卡尔乘积来表示所有可能状态的集合。

                (3.20)

基于单一状态  ，需要一个函数将所有状态的集合映射到一个子集，该子集包含所有非瞬时变换的状态。

                 (3.21)

                  (3.22)

就该示例而言，在系统的组件中可轻松定义此函数：

        (3.23)

根据所有的规则集，可计算出组件的最终变化状态（见方程式（3.16）至（3.19））。在这里，新的状态是根据当前的状态来计算的。需要注意的是，要保证  中只包含组件状态的唯一组合，从而能包含唯一的状态  。

变换。一旦模型还原完成，并且找到了所有状态的最小集合，就需要通过变换将这些状态连接起来。添加这些变换的过程非常琐碎。只要不存在或少存在一个变换，就有可能会多一个从状态  到状态  的变换，这个添加的过程可以通过可被利用的漏洞或修补，来触发状态的更改。例如，在状态  和  之间，只有一个组件可以独立地改变其状态以发生变换，即入接口  ，所有其他组件的状态都会根据定义的规则，随着  的变化而变化(见图1.3(b))。变换的频率被定义为组件的可被利用率  和修补率  。

示例。将上述映射函数应用到我们图1.1的例子中，从  开始，输入接口  与  的变换产生中间状态  ，触发ECU的子状态变换(见公式(3.16))  ，产生中间状态  。ECU的变换又触发出接口的子状态变换（见式（3.18））  ，产生状态变换为  。由于所有的规则都是一步到位的，所以模型中不再需要中间状态（见图1.3(b)）。