本文涵盖离散的以及连续的路径规划, 尽管现实世界是连续的, 但在很多情况下, 将世界离散化使得解决路径规划问题变得更加容易和快速.
学习路径规划, 主要的思考点有三个:
成本函数以及如何将人类洞察力(比如“右转比左转更容易”)纳入我们的规划算法
寻找最佳解决方案与寻找足够好的解决方案相关的最优性和权衡
在线算法与离线算法, 以及我们如何通过预先计算最佳路径尽可能避免路上的复杂计算
路径规划的目的是为了寻找成本最小的路径, 需要给出的条件包括: 地图, 起始地点, 目标地点, 成本函数.
1何理解成本函数?
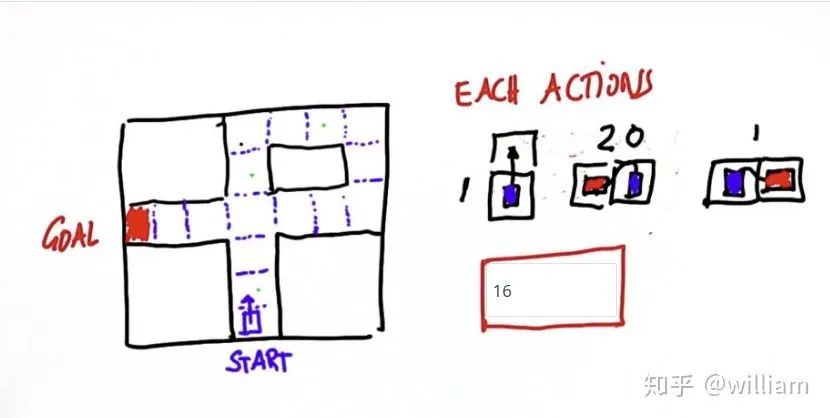
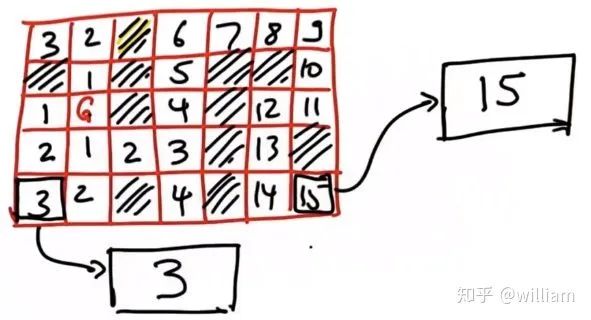
成本函数是基于人的安全驾驶行为的权衡, 最简单的例子是, 右转比左转方便, 在快递公司的路径规划中, 往往优先选择右转的道路, 因此我们可以假设左转的成本远高于右转. 如下图, 在交叉路口右转绕路的成本为16, 却低于左转的总成本, 为最优路径.
启发函数(Heuristic function)是一个有关我们距离目标多远的乐观猜测.它使用一个简单的欧几里得距离作为启发值来找出到达目标的路径.
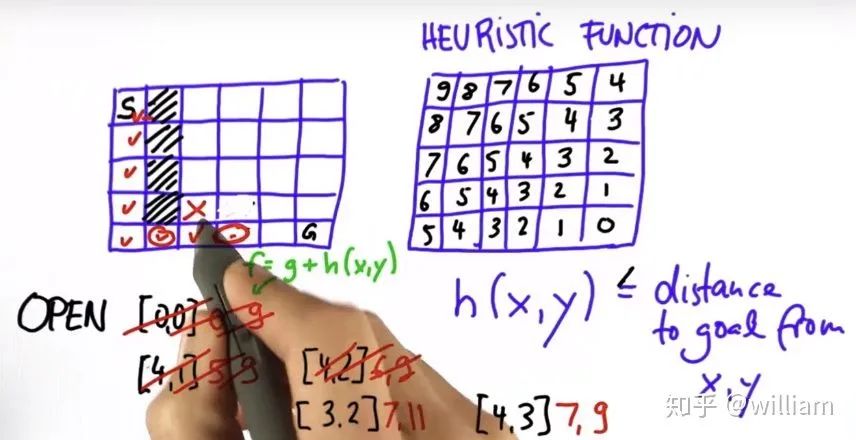
启发值h(x,y)的结果比实际距离小, 最佳情况是与实际距离相等.g value 实际是到这个位置的已经付出去的代价.启发函数为f = g + h(x,y) .如上图, 假设每步的代价是1, 从S位置到[3,2]的步骤是7步, 它的启发值是4, 因此总成本是11, 从S位置到[4,3]的步骤也是7步, 然而启发值仅为2, 总成本为9, 低于移动到[3,2]的成本, 因此[4,3]为最佳路径点.
执行代码:
# -----------
# User Instructions:
#
# Modify the the search function so that it becomes
# an A* search algorithm as defined in the previous
# lectures.
#
# Your function should return the expanded grid
# which shows, for each element, the count when
# it was expanded or -1 if the element was never expanded.
#
# If there is no path from init to goal,
# the function should return the string 'fail'
# ----------
grid = [[0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0]]
heuristic = [[9, 8, 7, 6, 5, 4],
[8, 7, 6, 5, 4, 3],
[7, 6, 5, 4, 3, 2],
[6, 5, 4, 3, 2, 1],
[5, 4, 3, 2, 1, 0]]
init = [0, 0]
goal = [len(grid)-1, len(grid[0])-1]
cost = 1
delta = [[-1, 0 ], # go up
[ 0, -1], # go left
[ 1, 0 ], # go down
[ 0, 1 ]] # go right
delta_name = ['^', '<', 'v', '>']
def search(grid,init,goal,cost,heuristic):
# ----------------------------------------
# modify the code below
# ----------------------------------------
closed = [[0 for col in range(len(grid[0]))] for row in range(len(grid))]
closed[init[0]][init[1]] = 1
expand = [[-1 for col in range(len(grid[0]))] for row in range(len(grid))]
action = [[-1 for col in range(len(grid[0]))] for row in range(len(grid))]
x = init[0]
y = init[1]
g = 0
h=heuristic[x][y]
f=g+h
open = [[f,g,h, x, y]]
found = False # flag that is set when search is complete
resign = False # flag set if we can't find expand
count = 0
while not found and not resign:
if len(open) == 0:
resign = True
return "Fail"
else:
open.sort()
open.reverse()
next = open.pop()
x = next[3]
y = next[4]
g = next[1]
expand[x][y] = count
count += 1
if x == goal[0] and y == goal[1]:
found = True
else:
for i in range(len(delta)):
x2 = x + delta[i][0]
y2 = y + delta[i][1]
if x2 >= 0 and x2 < len(grid) and y2 >=0 and y2 < len(grid[0]):
if closed[x2][y2] == 0 and grid[x2][y2] == 0:
g2 = g + cost
h2=heuristic[x2][y2]
f2=g2+h2
open.append([f2,g2,h2, x2, y2])
closed[x2][y2] = 1
for i in range(len(expand)):
print(expand[i])
return expand
search(grid,init,goal,cost,heuristic)
-------------------------------------
result:
[0, -1, -1, -1, -1, -1]
[1, -1, -1, -1, -1, -1]
[2, -1, -1, -1, -1, -1]
[3, -1, 8, 9, 10, 11]
[4, 5, 6, 7, -1, 12]
-1 代表障碍物或者不用去探索的区域.从0到12代表最佳的路径.
DRAPA 城市挑战赛斯坦福车辆用的正式A-star算法

动态规划是一种计算量密集的算法, 只需要基于目标点和地图, 就能输出从任何地点出发到目标点的最佳路径.我们需要用动态规划计算出优化策略(Policy).如下图所示:
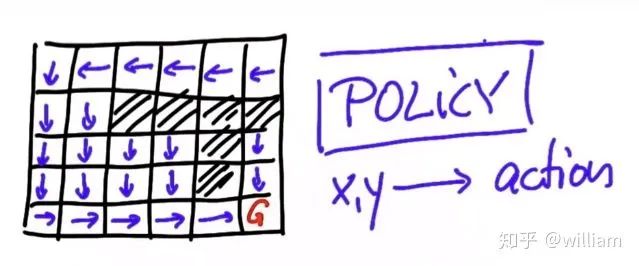
首先我们需要了解什么是最优策略:
最优策略会给每个单元格赋予一个动作.而价值函数会给每个单元格赋予一个值, 等于单元格到目标的最短距离.
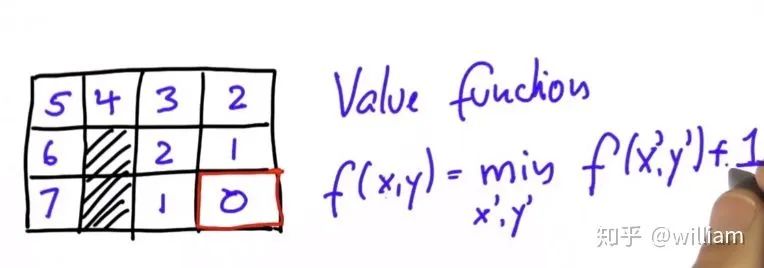
如上图计算到0点的最短距离, 把相邻单元格的值作为输入, 考虑它的值并加上到达它们的成本值(假设为1), 通过递归的使用这个价值函数, 获得每个单元格的最小化价值, 从而得到最优的动作策略.
代码:(假设每个单元格的初始值为99, 通过价值函数计算出最优价值)
# ----------
# User Instructions:
#
# Write a function optimum_policy that returns
# a grid which shows the optimum policy for robot
# motion. This means there should be an optimum
# direction associated with each navigable cell from
# which the goal can be reached.
#
# Unnavigable cells as well as cells from which
# the goal cannot be reached should have a string
# containing a single space (' '), as shown in the
# previous video. The goal cell should have '*'.
# ----------
grid = [[0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0]]
init = [0, 0]
goal = [len(grid)-1, len(grid[0])-1]
cost = 1 # the cost associated with moving from a cell to an adjacent one
delta = [[-1, 0 ], # go up
[ 0, -1], # go left
[ 1, 0 ], # go down
[ 0, 1 ]] # go right
delta_name = ['^', '<', 'v', '>']
def optimum_policy(grid,goal,cost):
# ----------------------------------------
# modify code below
# ----------------------------------------
value = [[99 for row in range(len(grid[0]))] for col in range(len(grid))]
policy = [['' for row in range(len(grid[0]))] for col in range(len(grid))]
change = True
while change:
change = False
for x in range(len(grid)):
for y in range(len(grid[0])):
if goal[0] == x and goal[1] == y:
if value[x][y] > 0:
value[x][y] = 0
policy[x][y]='*'
change = True
elif grid[x][y] == 0:
for a in range(len(delta)):
x2 = x + delta[a][0]
y2 = y + delta[a][1]
if x2 >= 0 and x2 < len(grid) and y2 >= 0 and y2 < len(grid[0]) and grid[x2][y2] == 0:
v2 = value[x2][y2] + cost
if v2 < value[x][y]:
change = True
value[x][y] = v2
policy[x][y]=delta_name[a]
return policy,value
policy,value=optimum_policy(grid,goal,cost)
for i in range(len(value)):
print(value[i])
for i in range(len(policy)):
print(policy[i])
-----------------------------
results:
[11, 99, 7, 6, 5, 4]
[10, 99, 6, 5, 4, 3]
[9, 99, 5, 4, 3, 2]
[8, 99, 4, 3, 2, 1]
[7, 6, 5, 4, 99, 0]
['v', '', 'v', 'v', 'v', 'v']
['v', '', 'v', 'v', 'v', 'v']
['v', '', 'v', 'v', 'v', 'v']
['v', '', '>', '>', '>', 'v']
['>', '>', '^', '^', '', '*']
A-star 算法是非结构化环境(停车场)中路径探索的最佳算法之一, 但是A-star 算法是离散的, 而机器人世界需要连续性. 因此我们基于运动学方程设计了混合A-Star, 从而使轨迹变得平滑.

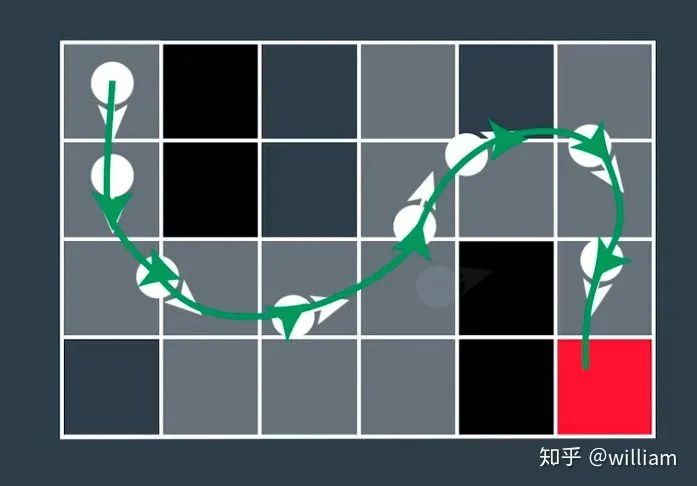
以上介绍的都是非结构化环境的路径搜索及运动规划的算法, 对于结构化的环境如高速公路, 由于存在很多特定的规则和参考路径, A-star算法不再适合。